Tests¶
melo has a standard set of unit tests, whose current CI status is:
The unit tests do not check the physical accuracy of the model which is difficult to verify automatically. Rather, this page shows a number of visual tests which can be used to access the model manually.
Toy model¶
Consider a fictitious “sports league” of eight teams. Each team samples points from a Poisson distribution \(X_\text{team} \sim \text{Pois}(\lambda_\text{team})\) where \(\lambda_\text{team}\) is one of eight numbers
specifying the team’s mean expected score. I simulate a series of games between the teams by sampling pairs \((\lambda_\text{team1}, \lambda_\text{team2})\) with replacement from the above values. Then, for each game and team, I sample a Poisson number and record the result, producing a tuple
where time is a np.datetime64 object recording the time of the comparison, \(\text{team1}\) and \(\text{team2}\) are strings labeling each team by their \(\lambda\) values, and \(\text{score1}\) and \(\text{score2}\) are random integers. This process is repeated \(\mathcal{O}(10^6)\) times to accumulate a large number of games.
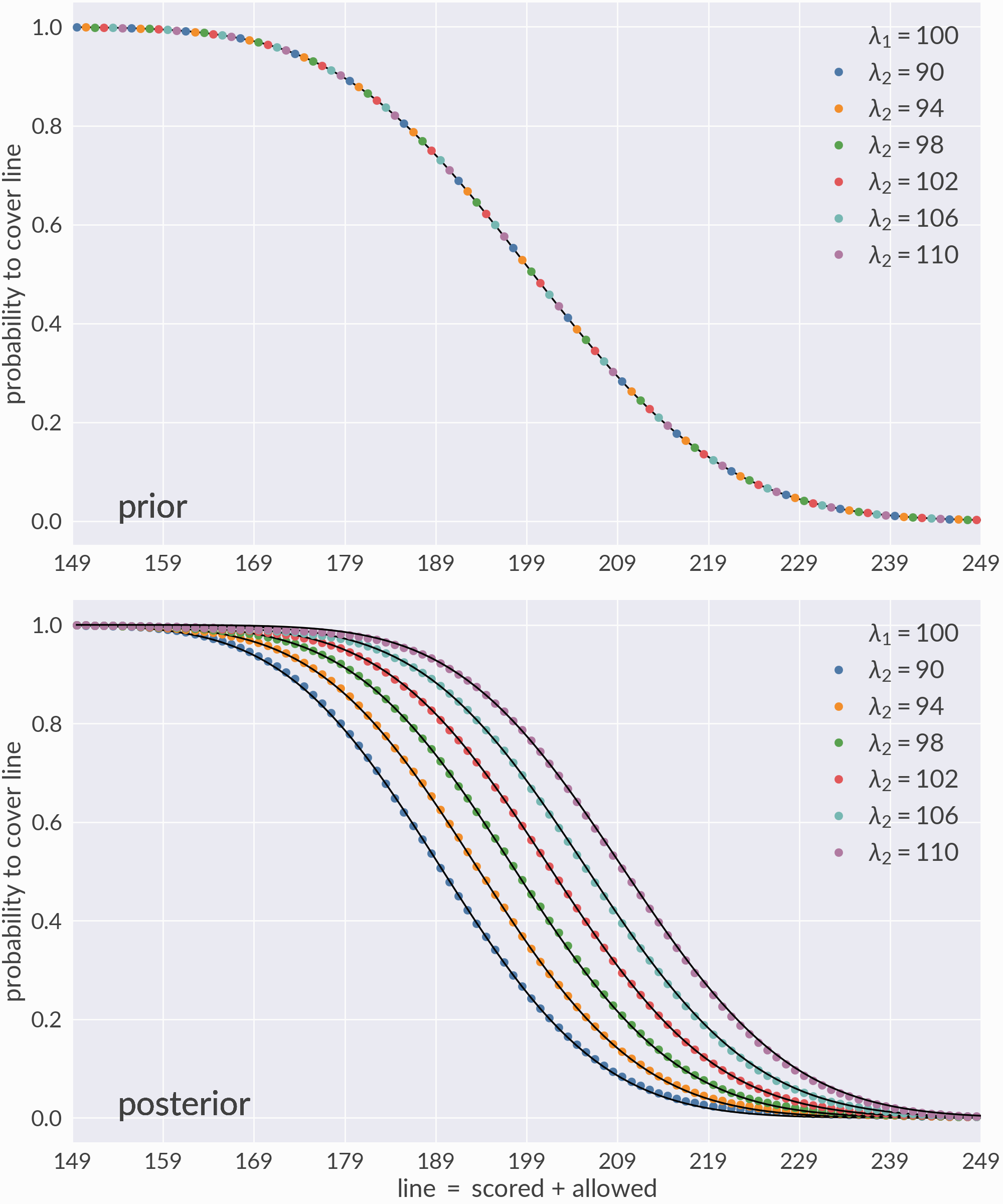
Point spread validation¶
I then calculate the score difference or \(\text{spread} \equiv \text{score1} - \text{score2}\) for each game to form a list of comparisons \((\text{time}, \text{team1}, \text{team2}, \text{spread})\) and use these comparisons to train the margin-dependent Elo model:
lines = np.arange(-49.5, 50.5)
model = Melo(1e-4, lines=lines, commutes=False)
model.fit(times, teams1, teams2, spreads)
Now that the model is trained, I can predict the probability that various matchups cover each value of the line, i.e. \(P(\text{spread} > \text{line})\). Since the underlying distributions are known, I can validate these predictions using their analytic results.
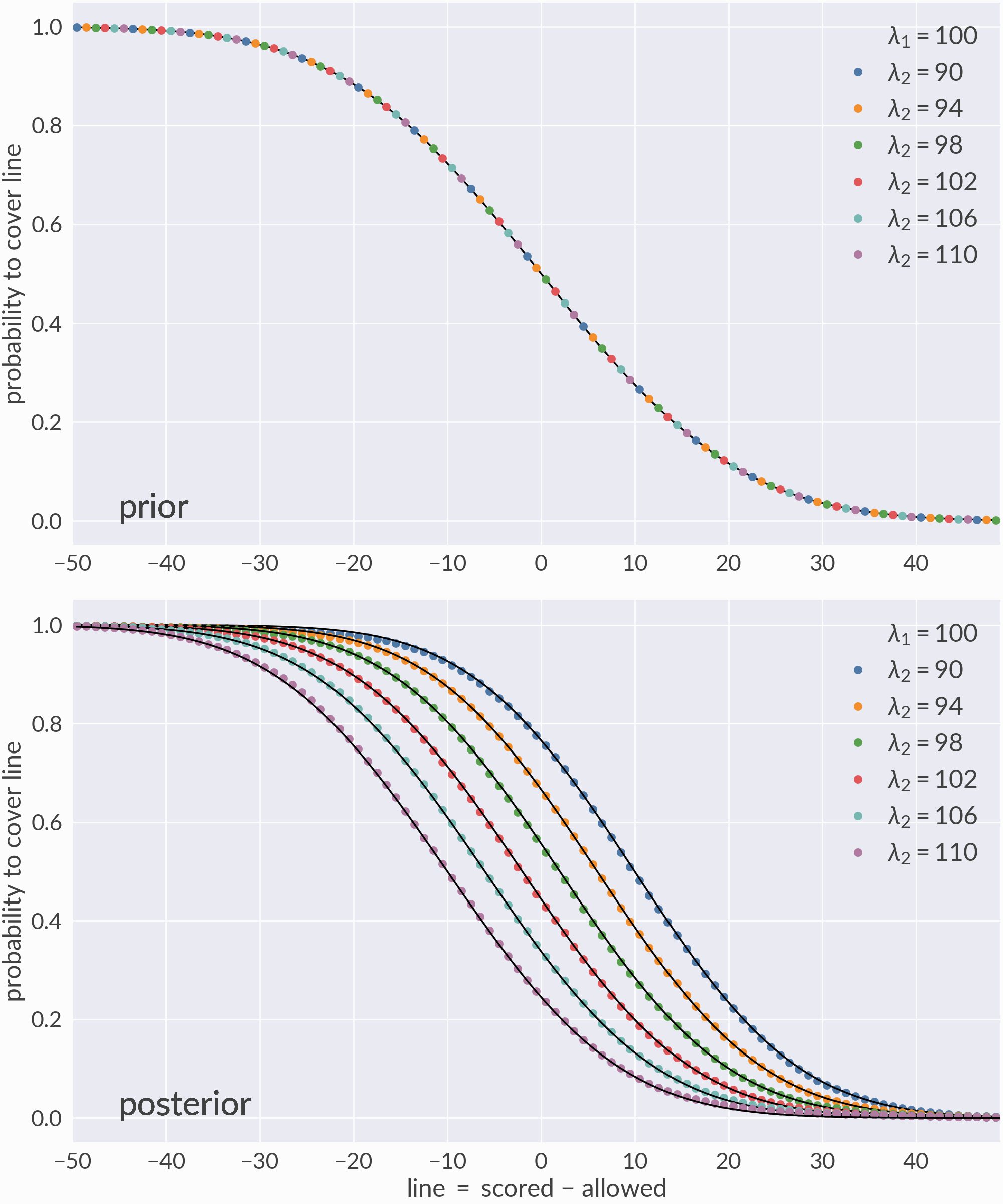
The top panel validates the model’s prior predictions (before the first game), and the bottom panel validates its posterior predictions (after the last game). The colored dots are model predictions and the black lines are their target values.¶